5 класс
- В записи 88888888 расставьте между некоторыми цифрами знаки сложения так, чтобы получилось выражение, значение которого равно 1000.
- Для нумерации книги для детей понадобилось 204 цифры. Сколько страниц в книге, если нумерация книги начинается с первой страницы?
- В квартирах №1, №2, №3 жили три котенка: белый, черный и рыжий. В квартирах №1 и №2 жил не черный котенок. Белый котенок жил не в квартире №1. В какой квартире жил каждый котенок?
- Даны числа от 1 до 9 . Расставьте их в кружки так, чтобы сумма трех чисел вдоль каждой линии была равна 15. Какое число должно быть в центре?
- У одного мальчика нет братьев, а у его сестры братьев столько же, сколько сестер. Сколько детей в семье?
- Когда у рыбака спросили, как велика пойманная им щука, он сказал: «Я думаю, что хвост ее – кг, голова – столько, сколько хвост и половина туловища, а туловище – сколько голова и хвост вместе». Сколько весит щука?
7.Разрежьте квадрат размером 4 х 4 на 4 равные фигуры. Резать можно только по сторонам клеточек. Найдите как можно больше способов.
7 класс
- В ящике имелись апельсины и лимоны, причём число лимонов составляло числа апельсинов. Когда из ящика достали 7 лимонов и 15 апельсинов, то число лимонов составило от числа оставшихся апельсинов. Сколько лимонов и сколько апельсинов было в ящике?
- Расшифруйте числовой ребус АЛЛО·Я = ЭЛЛА, в котором буквами А, Л, О, Э, Я обозначены различные нечётные цифры.
- В корзине лежат подосиновики и подберезовики – всего 30 штук. Известно, что, какие бы 12 грибов ни достать из корзины, среди них окажется по крайней мере один подосиновик. А если произвольно достать 20 грибов, то среди них будет по крайней мере один подберезовик. Сколько подосиновиков в корзине?
- Эта игра является самым простым из многочисленных вариантов древней восточной игры Hим. Hа столе лежит куча камешков. Каждый игрок по очереди берет из кучи от 1 до 3 камешков. Выигрывает тот, кто последним сделает ход. В одном из pозыгpышей победил тот игрок, который ходил первым, причем он был уверен в выигрыше с самого начала. Определите, какая была куча — 32 камешка, 36 камешков, или 54 камешка? Объясните свое решение.
8 класс
- Найдите все положительные четырёхзначные числа, у которых суммапервых трёх цифр равнв 2, сумма последних трёх цифр равна 5, а сумма первой и последней цифр делится на 7.
- Социологи провели опрос » Что вы предпочитаете пить по утрам: чай или кофе?» 37,5% опрошенных ответили «чай»,56,25% опрошенных ответили «кофе», а 9 человек не ответили ничего. Сколько человек опросили социологи?
- В выпуклом четырёхугольнике АBCD диагональ АС является биссектрисой углов А и С. Докажите, что если две противолежащие стороны четырёхугольника равны, то диагональ ВD является биссектрисой углов В и D.
- Четырёхзначное число разложили на простые множители. Затем цифры заменили буквами (различным буквам соответствуют различные цифры) и получили равентво АБВГ = Г * ВВ * ДВ. Восстановите данное разложение.
- На каждой из шести граней куба написано натуральнае число. Затем для каждой вершины куба подсчитывается произведение чисел, написанных на трёх гранях, имеющих эту вершину общей точкой. Оказалось, что сумма таких произведений равна 1001. Какова сумма чисел, написанных на гранях куба?
9 класс
- Вычислите:
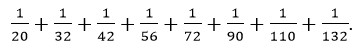
- В треугольнике ABC проведены биссектрисы углов A и B, угол между ними равен 1250. Найдите угол C.
- Постройте график функции
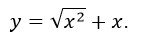 .
. - Решите уравнение
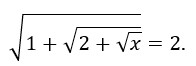
- Найдите значения a и b, при которых равенство
 выполняется при всех допустимых значениях переменной x.
выполняется при всех допустимых значениях переменной x.

























.jpg)












